単位換算が苦手な人必見見るだけで覚える早見表と忘れない方法！

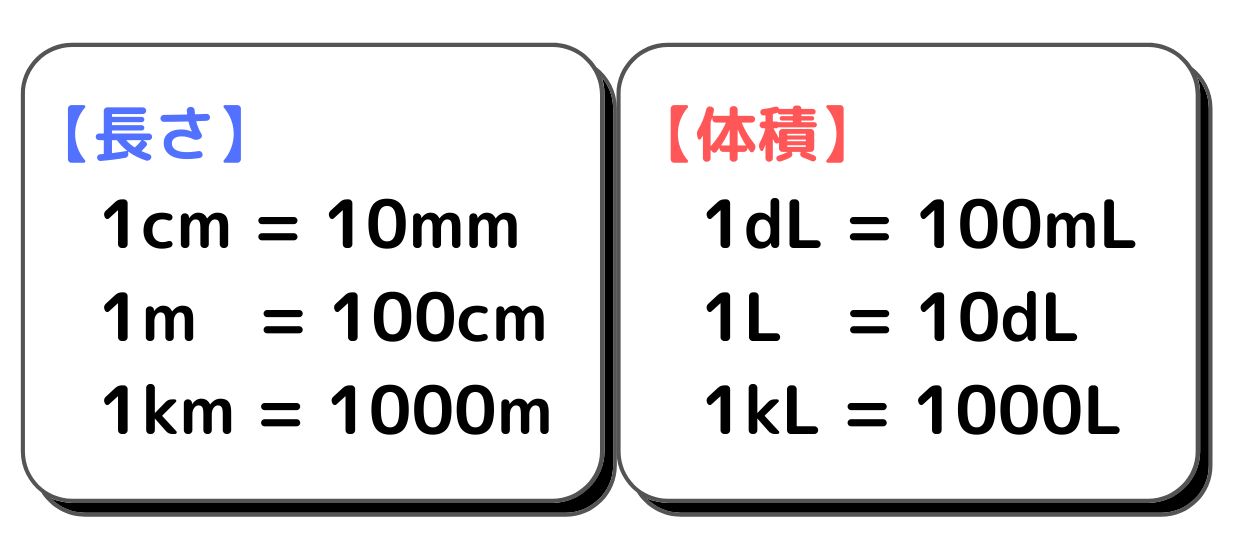
「1キロメートルって何メートルに相当するんだっけ？」「1リットルをミリリットルで表すといくつになる？」──日常生活や仕事の場面で、こういった基本的な疑問に直面して戸惑った経験はないでしょうか？

単位の換算という分野は、義務教育の過程で必ず学習する内容であるにもかかわらず、実際の場面で活用しようとすると頭が混乱してしまう、そんな不思議なテーマの代表格と言えます。

でも心配する必要はありません。なぜなら、あなたが苦手意識を持っているのは、決して理解力や記憶力に問題があるわけではないからです。実は、多くの方が陥っている「丸暗記に頼った学習法」こそが、混乱の最大の原因になっています。

本記事では、記憶力だけに頼るのではなく「本質を理解しながら自然に身につける」というアプローチで、単位換算をマスターする手法をお伝えしていきます。

特にご紹介したいのが、「小数点スライド法」と呼ばれる画期的な考え方。この手法を使えば、あらゆる単位の変換が「右方向に動かすのか、それとも左方向に動かすのか」という単純な判断だけで完結してしまうんです。

加えて、本記事では長さ・重さ・面積・体積・時間といった各カテゴリーごとに、視覚的に理解できる早見表も豊富に用意しています。これらの表を眺めるだけで、単位同士の関係性が直感的に掴めるように設計しました。

この記事を最後まで読み進めていただければ、今まで「苦手」「面倒」と感じていた単位換算が、「得意」「簡単」なものへと変化していくはずです。

数字や単位がスムーズに頭の中で処理できる、そんな爽快な感覚をぜひ体験してみてください。

なぜ多くの人が単位換算を難しく感じてしまうのか？

単位の換算作業に対して「難しい」「ややこしい」という印象を持つ方は、想像以上に大勢いらっしゃいます。

ただし、これは知的能力や頭の良し悪しとは全く関係のない話です。

実のところ、大半の方が陥っている落とし穴は「とにかく数字を覚えればなんとかなるだろう」という、暗記中心の学習姿勢にあります。

単位換算でつまずく本当の理由とは何か？

単位の変換作業で多くの人が行き詰まってしまう最大の原因は、「桁がどう移動するのか」「接頭語が何を意味しているのか」という根本的な仕組みを理解しないまま、ただひたすら数字だけを頭に詰め込もうとすることにあります。

例を挙げてみましょう。「1km＝1000m」という公式を覚えている人は多いでしょう。けれども、「どうして1000という数字になるのか」という理由まで把握している人は少ないかもしれません。

この「なぜ？」の部分が曖昧なままだと、問題の出され方が少し変わっただけで、途端に何をすればいいのか分からなくなってしまいます。

暗記だけに頼った知識は応用が効きにくいため、感覚レベルでの理解が欠かせません。

この「理解の不足」こそが、多数の学習者にとって単位換算を難しく感じさせている根本的な要因となっているわけです。

よくあるつまずきポイント	その背景にある原因
ゼロの個数を取り違える	接頭語が示す倍率の意味を把握できていない
平方メートル・立方メートルなどで混乱する	「2乗」「3乗」という概念を意識的に捉えていない
時間に関する換算が特に苦手	10進法と60進法の区別を整理できていない

丸暗記ではなく「構造の理解」が成功への鍵を握る理由

単位換算を「一度学んだら忘れない知識」として定着させるために最も大切なのは、数字と数字の間にある関係性を、イメージとして頭の中に描けるようになることです。

具体的に言うと、「キロ」や「ミリ」といった言葉が、それぞれ何倍の関係を示しているのかを知るだけで、換算のメカニズムが驚くほど明瞭になります。

仕組みを理解できてしまえば、暗記しようと努力しなくても、自然と知識が頭に残るようになります。

つまり、単位換算の核心は「数字を覚える作業」ではなく、「関係性を可視化すること」だと言えるでしょう。

最初に押さえておきたい単位換算の基礎知識と接頭語の役割

単位の換算作業を始める際の第一歩は、基本となる単位と接頭語がどんな関係にあるのかを知ることです。

この土台部分をしっかり押さえるだけで、一見複雑に見える計算の大部分が、実は非常にシンプルな構造であることが見えてきます。

「メートル」「グラム」「リットル」を軸に考える思考法

単位の世界における中心的な存在となるのが、「メートル（m）」「グラム（g）」「リットル（L）」という3つの基本単位です。

これらはそれぞれ「長さ」「重さ」「体積」という異なる物理量の基準を表しています。

そして、こうした基本単位の前に「キロ」「センチ」「ミリ」などの接頭語を付け加えることによって、10倍・100倍・1000倍といった倍率関係を表現する仕組みになっているわけです。

基本となる単位	表している物理量	具体例
メートル（m）	長さの基準	1m＝100cm
グラム（g）	重さの基準	1g＝1000mg
リットル（L）	体積の基準	1L＝1000mL

「キロ」「センチ」「ミリ」などの接頭語が持つ意味を整理する

接頭語は、単位換算という分野における最も根幹的な要素です。

この部分を正確に理解しておくと、どんな単位の組み合わせに遭遇しても、迷うことがなくなります。

接頭語	読み方	表す倍率	使用例
キロ（k）	きろ	1000倍	1km＝1000m
ヘクト（h）	へくと	100倍	1ha＝100a
デカ（da）	でか	10倍	1dal＝10L
デシ（d）	でし	1/10倍	1dL＝0.1L
センチ（c）	せんち	1/100倍	1cm＝0.01m
ミリ（m）	みり	1/1000倍	1mm＝0.001m

この一覧表は、単位換算における「辞書」のような役割を果たすものです。

接頭語の意味を正確に把握できれば、単位と単位の関係が一目瞭然になります。

この基礎的な部分をマスターした上で、次のセクションでは各ジャンルごとの「瞬時に理解できる早見表」をご紹介していきます。

各ジャンルごとに整理！視覚的に理解できる単位換算完全ガイド

ここからは、実際に使われる単位の換算をカテゴリーごとに分類して整理していきます。

各表は「眺めるだけ」で単位同士の関係性が直感的に分かるように構成していますので、無理に暗記しようとしなくても自然と理解が深まっていきます。

【長さに関する単位】km・m・cm・mmの相互関係と記憶のコツ

長さを表す単位は、私たちの日常生活の中で最も頻繁に登場する計測単位です。

「キロメートル」「メートル」「センチメートル」「ミリメートル」といった単位の関係を記憶するコツは、小数点の位置がどう移動するかを意識することにあります。

単位の名称	記号	他の単位との関係	日常的なイメージ
キロメートル	km	1km＝1000m	小学校のグラウンドを4周する距離
メートル	m	1m＝100cm	成人男性が一歩踏み出す歩幅
センチメートル	cm	1cm＝10mm	人差し指の横幅程度
ミリメートル	mm	1mm＝0.1cm	シャープペンシルの芯の太さ

表の右側に進むほど小数点を右方向へ、左側に進むほど左方向へスライドさせる、というのがポイントになります。

この「小数点を動かすイメージ」を頭の中に持つだけで、桁数の移動が格段にスムーズになります。

【重さに関する単位】t・kg・g・mgを具体的イメージで把握する

重さを示す単位も、基本的には1000倍という関係性で結びついています。

実際の重量を身近な物体と結びつけてイメージすると、格段に記憶に定着しやすくなります。

単位の名称	記号	他の単位との関係	日常的なイメージ
トン	t	1t＝1000kg	軽自動車1台分の重量
キログラム	kg	1kg＝1000g	牛乳パック1リットルの重さ
グラム	g	1g＝1000mg	1円硬貨1枚の重さ
ミリグラム	mg	1mg＝0.001g	医薬品に含まれる有効成分の量

例えば、1kgをmgに変換したい場合は、右方向に3段階スライドする（1000×1000×1000＝1,000,000,000倍）というイメージで捉えます。

このように、接頭語の段階を頭の中で「横にスライドさせる」感覚を持つと、瞬時に換算が可能になります。

【面積と体積の単位】2乗・3乗を図形でイメージする技術

面積や体積の計算に入ると、掛け算の回数が増えるため混乱を招きやすいですよね。

ただし、メカニズム自体はシンプルで、「平方（2乗）」「立方（3乗）」を掛け合わせるだけでOKです。

分類	単位の変換	換算の関係	記憶のポイント
面積	m²→cm²	1m²＝10,000cm²	100×100＝10,000倍
体積	m³→cm³	1m³＝1,000,000cm³	100×100×100＝1,000,000倍

つまり、「1mをcmに換算すると100倍」という関係があるならば、「1m²をcm²に換算すると100×100倍」、「1m³をcm³に換算すると100×100×100倍」になるわけです。

乗数が増えるたびにスライドの回数も増える、という感覚を持てば、混乱を避けることができます。

【時間の単位】時・分・秒の変換をミスせず行うテクニック

時間に関する換算だけは、通常の10進法ではなく「60進法」で動く特殊なパターンになっています。

ただし、ルールを理解してしまえば、それほど難しくありません。

変換の方向	計算の方法	具体例
時間 → 分	×60	2時間＝120分
分 → 秒	×60	3分＝180秒
秒 → 分	÷60	180秒＝3分
分 → 時間	÷60	150分＝2.5時間

時間だけは小数点のスライドではなく、「60という数字を基準に考える」ことがコツです。

この違いを認識しておくだけで、計算ミスを大幅に減らすことができます。

魔法のような法則「右か左かの判断だけ」で全ての単位換算が可能に！

ここまでの内容を統合すると、ほぼ全ての単位換算は「右方向か左方向に動かすだけ」で成立するということが分かります。

これこそが、あらゆる単位に応用可能な小数点スライド法の真髄です。

小数点を移動させるだけで理解できる万能パターン

「小さな単位に変更する際は右方向へ」「大きな単位に変更する際は左方向へ」この動きの原理さえ理解していれば、どんな換算問題にも対応できてしまいます。

動きの方向	行う操作	結果として起こること	具体例
右へ進行する	小数点を右へ移動	数値が大きくなる	1m → 100cm
左へ戻る	小数点を左へ移動	数値が小さくなる	1000g → 1kg

「右に動かすべきか、それとも左に動かすべきか」という判断だけで済むという単純明快さが、この手法の最大の利点です。

接頭語の倍率を完璧に記憶していなくても、スライドする方向さえ分かっていれば自然と正解に辿り着けます。

2乗・3乗にも対応できる「小数点スライド法」の応用

この法則は、面積や体積といった複雑な単位にも応用できます。

例えば、1m²をcm²に変換するなら100を2回掛ける（つまり右に2段階スライド）、1m³をcm³に変換するなら100を3回掛ける（右に3段階スライド）と考えればいいわけです。

単位の換算内容	スライドする回数	最終的な結果
1m → cm	1回（2桁）	1m＝100cm
1m² → cm²	2回（4桁）	1m²＝10,000cm²
1m³ → cm³	3回（6桁）	1m³＝1,000,000cm³

「乗数が増加する＝スライド回数が増加する」という原理を把握すれば、複雑に見える単位換算も恐れる必要がありません。

つまり、単位換算は暗記作業ではなく、スライドの感覚で身につけるのが正攻法というわけです。

単位換算でよく発生する間違いとその解決策

どれだけ理論を理解していても、実際の計算の場面でつまずくことはあります。

このセクションでは、単位換算において多くの学習者が犯しやすいミスと、それを未然に防ぐための具体的な方法をご紹介します。

ゼロの個数を取り違える原因と予防策

最も頻繁に発生するのが「0（ゼロ）の個数を間違える」というミスです。

1km＝1000m、1m＝100cm、1cm＝10mmと覚えていても、ゼロの数を正確に把握していないと、計算結果が大きくズレてしまいます。

特に、100倍と1000倍を混同してしまうケースが非常に多く見られます。

間違いやすい例	正しい換算式	確認の方法
1km＝100m	1km＝1000m	「キロは3つのゼロ！」と声に出して確認
1cm＝1000mm	1cm＝10mm	「センチは1桁だけスライド」と言葉で確認

対策としては、声に出してゼロの数を確認するという方法があります。

人間の脳は「視覚だけ」よりも「音声化する」方が記憶に定着しやすい性質を持っているため、声に出すことで桁数を間違えるリスクが減少します。

「2乗」「3乗」を忘れないための視覚的トレーニング方法

面積（m²）や体積（m³）の換算では、「2乗」や「3乗」という概念を忘れてしまう人が多数います。

これは、数値の動きを立体的にイメージできていないことが原因です。

そこでおすすめしたいのが、「目で見る立体トレーニング」という手法です。

単位	意味している内容	日常的なイメージ
1m²	1m×1mの正方形	畳1枚弱の広さ
1m³	1m×1m×1mの立方体	浴槽1杯分の容積

このように、数字を「立体的な形」として捉えることで、「2乗」「3乗」という言葉が自然と体感的に理解できるようになります。

紙に立方体を描いたり、ブロックを使って立体を組み立てるだけでも、驚くほど効果が得られます。

一度身につけたら忘れない！単位換算を定着させる実践的トレーニング

習得した単位換算の知識を「一生使える技術」にするためには、日常生活の中で繰り返し触れることが大切です。

このセクションでは、無理なく継続できる実践的なトレーニング方法と便利なツールをご紹介します。

日常生活の中で自然に練習できる「単位意識化」テクニック

単位換算をマスターするコツは、「勉強として取り組まない」ことです。

普段の生活でちょっとした瞬間に単位を意識するだけで、自然と技術が身についていきます。

場面	意識する単位	具体例
スーパーマーケットでの買い物	mL・L	500mLのペットボトル＝0.5L
料理をする時	g・mL	大さじ1＝15mL、小さじ1＝5mL
ジョギングやランニング	m・km	3km走る＝3000m
ニュースを視聴する時	m/s	台風の風速20m/s＝時速72km/h

「これって何mLになるんだっけ？」と自問自答するだけでも、単位換算の感覚がどんどん研ぎ澄まされていきます。

まるで筋力トレーニングのように、日々の小さな積み重ねが確実な定着へとつながっていきます。

無料プリント・アプリ・ツールで効率的に復習する方法

現在は、単位換算の練習をサポートしてくれる無料のツールも充実しています。

自分のペースに合った手段を選び、隙間時間に繰り返し練習するのがおすすめです。

タイプ	内容	特徴
練習プリント	単位換算の問題集＋解答付き	紙媒体で繰り返すと記憶が定着しやすい
スマートフォンアプリ	単位換算クイズ・タイムアタック形式	ゲーム感覚で楽しく続けられる
オンラインツール	自動換算機能＋早見表	仕事や学習時にすぐ活用できる

特におすすめなのが、スマートフォンアプリでのクイズ形式です。

遊びながら学べる環境は、モチベーションを長期間維持するための鍵になります。

「ちょっとだけやってみようかな」という軽い気持ちでスタートして大丈夫です。

小さな積み重ねが、確実な「単位換算力」へとつながっていきます。

最後に

ここまで、単位換算を瞬時に理解し記憶するための考え方と実践法をお伝えしてきました。

最後にもう一度、本質的なポイントを整理しておきましょう。

ポイント	詳細な内容
① 暗記より理解を優先	接頭語と構造を理解すれば、桁の移動が自然に分かるようになる
② 小数点スライド法の活用	右か左かの判断だけで、あらゆる換算に対応できる
③ イメージによる記憶	具体的な物や距離と結びつけると忘れにくくなる
④ 日常での反復練習	生活の中で「単位を意識する習慣」をつける

単位換算は、最初こそ複雑に思えるかもしれませんが、仕組みを理解すれば驚くほどシンプルです。

大切なのは、数字を単なる記号として覚えるのではなく、意味とつながりで捉えること。

そして、「小数点を右に動かす」「左に動かす」という感覚を自然に身につけることです。

本記事でご紹介した手法を実践すれば、もう単位換算に苦手意識を感じることはないでしょう。

理解・イメージ・反復という3つの要素を意識すれば、あなたも今日から単位換算の達人になれます。

数字や単位に自信がつくと、勉強や仕事、そして日常生活のあらゆる場面で迷いがなくなります。

あなたの中に眠っている「単位を扱う力」を、今この瞬間から鍛えていきましょう。